SUNY Geneseo Department of Computer Science

A Board Game Example of Dynamic Programming

Return to List of Lectures

Misc

Dynamic programming problem set (problem set 7) now due next Monday, March 11

I’m out of town Thursday (Mar. 7)

• More specifically, from this afternoon through Friday
• “Class” will be on-line discussion of the requirements for problems to be solvable by dynamic programming
• Read section 15.3 (it has more references than I would like to the matrix chain multiplication example that we haven’t studied yet, but the core ideas in this section are independent of any specific dynamic programming application, and so hopefully the section will be intelligible even if you have to skip over references to that particular example).
• Then discuss the questions in the dynamic programming wiki on our “Course Materials” tab at myCourses
  • Discussion will probably be most beneficial if you do it in a number of small pieces over the next 4 days or so, rather than trying to do it all at once in one long session

Questions?

Dynamic Programming Problems

Problem 1 from problem set (tile game)

• Points are gained by moving between tiles, not just by being on a tile. Points may be negative as well as positive

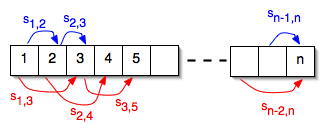
• Start developing an algorithm from the “top” down, i.e., start by thinking about maximum achievable score at some tile n
• It can be described recursively, in terms of maximum scores at each of the tiles you could reach n from
  • maxScore( n ) = max( s_n-1,n + maxScore( n-1 ), s_n-2,n + maxScore( n-2 ) )
  • maxScore( 1 ) = 0
  • maxScore( 2 ) = s_1,2
• Computing this recursively would be very expensive because of all the repeated calculations it would do
• Instead, make a table of maxScore values and fill it in from the base cases up to larger cases

        tiles( n, s )
            let N[1..n] be a new array        // N[i] will hold maxScore(i)
            N[1] = 0
            N[2] = s[1,2]
            for i = 3 to n
                N[i] = max( s[i-1,i] + N[i-1], s[i-2,i] + N[i-2] )
            return N

• This tells you the maximum achievable scores, but not how to achieve them. To do that, add an auxiliary array M such that M[i] is the tile you should move to i from

        tiles( n, s )
            let N[1..n], M[1..n] be new arrays        // N[i] will hold maxScore(i); M[i] will hold tile to go to i from
            N[1] = 0
            N[2] = s[1,2]
            M[2] = 1
            for i = 3 to n
                if s[i-1,i] + N[i-1] > s[i-2,i] + N[i-2]
                    N[i] = s[i-1,i] + N[i-1]
                    M[i] = i-1
                else
                    N[i] = s[i-2,i] + N[i-2]
                    M[i] = i-2
            return N, M

Problem 3 from problem set (seam carving)?

• The basic problem is to find a chain of adjacent pixels to remove from an image

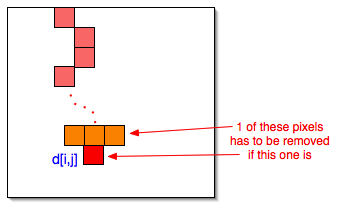
• Need a recursive definition of a “minimum seam distortion” function
  • The least distortion seam could end anywhere in the bottom row, so at least the column in which the seam ends has to be a parameter
  • But minimum distortion in one row is found by adding that pixel’s distortion to the minimum distortions of seams to its possible predecessors in the previous row, so row should be a parameter too
  • Recursive part of the recurrence is then
    • D(i,j) = d[i,j] + min( D(i-1,j-1), D(i-1,j), D(i-1,j+1) )

Next

(Tuesday, Mar. 12)

Matrix chain multiplication

Section 15.2