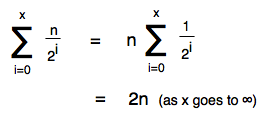SUNY Geneseo Department of Computer Science

Divide and Conquer

Return to List of Lectures

Questions?

Divide and Conquer

Median value in an unsorted array A[1..n] (or generally kth smallest, median is n/2-smallest)

• Naively, you could sort the array and then pick out the kth element
  • How long that would take depends on the sorting algorithm you use
  • Optimal sorting
    • Define sorting as
      • Array of n elements
      • Only 2-way compare and swap
    • Consider how many permutations of the array there can be, and how many comparisons it takes to determine which one you are dealing with

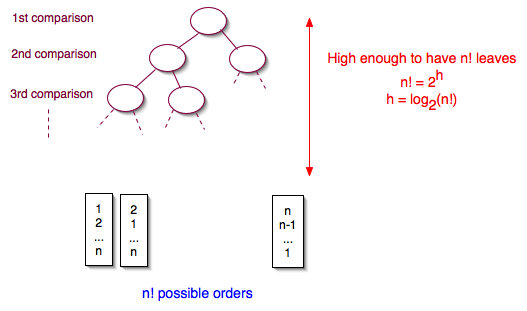
• log n!
  • = log(  √(2πn)(n/e)ⁿΘ(1) ) by Stirling’s formula (aka Stirling’s approximation), a formula useful enough that you should know that it exists, but you can look it up when you need it
  • ≈ log( c n^1/2 (n/e)ⁿ )
  • = logc + 1/2 logn + n( logn - loge )
  • = Θ( logn + nlogn - n )
  • = Θ( nlogn )
• So a naive kth-smallest algorithm would run in Θ( nlogn ) time
• Could you do better? Intuitively you might think that finding one element out of n shouldn’t take so long
• Divide-and-conquer idea: divide the array into the “small” elements and the “large” ones, and then recursively look in just one of those groups, according to how big k is. After some thinking and revising, this ends up looking like…

        kthSmallest( A, first, last, k )
            if last < first
                // array section is empty, error!
            else
                p = partition( A, first, last )        // as in Quicksort
                if k < p
                    kthSmallest( A, first, p-1, k )
                else if k > p
                    kthSmallest( A, p+1, last, k+p )
                else
                    return A[p]

• Intuitively, this should take time n to partition the whole array, then n/2 for one of the sections, then n/4 for a section of a section, and so on

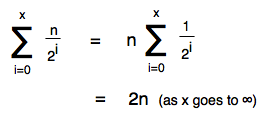
• But the algorithm still isn’t completely correct….

Hand out divide and conquer problem set

Next

How do you ensure that a divide-and-conquer algorithm is correct? Proof by induction!

No reading, but think about how you would prove the kth-smallest algorithm correct, and be ready to talk about doing it