SUNY Geneseo Department of Computer Science
CSci 120, Spring 2014
Prof. Doug Baldwin
Complete by Friday, March 14
“While” loops are mechanisms for repeating some group of statements a number of times, somewhat like “for” loops. The difference between “while” and “for” is that “for” repeats the statements a fixed number of times, whereas “while” repeats them as long as some condition is true. A “while” loop is thus appropriate when you know what circumstances you want to keep repeating under, but not how long those circumstances might last, and a “for” loop is appropriate when you know in advance the number of times or set of values on which you want to repeat.
The knowledge of Matlab that you will need for this lesson comes from the following sources:
Ask yourself how many times you will have to flip a coin before it comes up heads. You might get lucky, and have the coin produce heads on the first flip. Or you might get tails on the first flip and heads on the second, or two tails followed by heads on the third try, and so forth. In general, in order to need to flip the coin n times, you have to get tails on the first n-1 flips, and heads on the last. Intuitively, the probability of such a sequence of flips decreases as n increases. The graph of probability versus n is an example of a geometric distribution.
More formally, suppose you are doing an experiment that can either succeed or fail, with the probability of success being p, and the probability of failure thus being 1-p. Different instances of the experiment are independent of each other, i.e., whether earlier instances succeeded or failed doesn’t influence the chances of the next instance succeeding or failing. Each instance of such an experiment is known as a Bernoulli trial. For example, the coin-flipping scenario described above is a sequence of Bernoulli trials (i.e., of experiments as described here) with the probability of success (getting heads) being 1/2, and the probability of failure thus being 1 - 1/2 or 1/2 also.
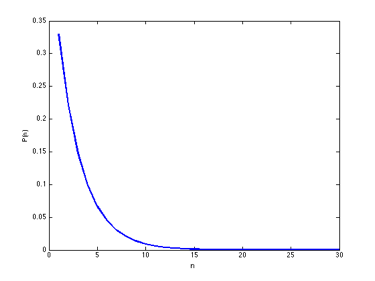
One can show that the probability of needing n Bernoulli trials in order to see the first success is p(1-p)n-1. This relation between n and its probability is a geometric distribution. Probability distributions are often written as equations defining P(n), the probability of a number, n, occuring. In the case of geometric distributions, these equations are of the form P(n) = p(1-p)n-1, for some given probability p.
As an example, here is a plot of a geometric distribution for p = 0.33:

Finally, one can also show that the expected number of Bernoulli trials needed in order to have the first success is 1/p. In other words, imagine doing a series of Bernoulli trials with success probability p until you have the first success, and then repeating that process many times: over all of the repetitions, the average number of Bernoulli trials needed in order to see the first success is expected to be 1/p.
Write a Matlab script that simulates series of Bernoulli trials. Specifically, your script should first ask its user for a probability, p. It should then simulate a large number (say, 1000) of series of Bernoulli trials with that probability that continue until encountering the first success. Use Matlab’s random number generator (the rand function) to generate an outcome for each Bernoulli trial. During this simulation, the script should count the number of series that need 1 trial, 2 trials, 3 trials, etc. At the end of the simulation, your script should plot the counts versus the number of trials—this plot should show an approximately geometric distribution.
I expect that you will need to put some thought into the algorithm on which to base your script before you start to write it. Use your study groups to help with this, i.e., talk over the algorithm with the rest of your group, and be sure that the group as a whole agrees on the algorithm, before you start to write code.
Because your script involves randomness, it may be hard to be sure that it works correctly. However, you can still use examples to test it (and to help ensure that you understand what you are to do). In particular, come up with some example probabilities, and for each figure out by hand what a geometric distribution of counts over 1000 (or whatever number you use) series of trials should look like (i.e., how many series should only contain 1 trial, how many should contain 2, and so forth, for a few selected numbers of trials). Compare these numbers to the numbers from your plots. No single run of your script should produce exactly the numbers from your examples, but if several runs are consistently off the example numbers (i.e., always lower than the examples, or always higher), you should suspect that something is wrong with your script.
When your script asks its user for a probability, the user should enter a number greater than 0 and less than or equal to 1. Include code in your script that checks to see if the user’s input in in this range, and keeps asking for input until it is.
Both of the examples of “while” loops in the Edinburgh mini-lecture could arguably be done more elegantly with “for” loops. Show what the examples would look like using “for” loops instead of “while” loops. What, if anything, does this suggest to you about the relationship between “while” and “for”?
In your study group’s first face-to-face meeting with me following your “Complete By” date above, I will look over your solutions to the exercise, ask you any further questions I have, and answer any questions from you. I may also ask you to demonstrate your script in Matlab. Please bring at least one copy of the “.m” file containing this script to your meeting. This will speed the meeting along.