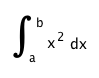
SUNY Geneseo Department of Computer Science

Lesson 7—For Loops and Riemann Sums

Purpose

Background

The basic knowledge of Matlab and integration that you will need for this lesson comes from the following sources:

• Chapter 5 up to but not including section 5.2.1 of Attaway
• The “Programming introduction” and “For loops” sections (under “Programming”) in the “Logic and Control Flow” chapter from the Mathworks tutorials.
• Khan Academy lectures on Riemann sums: 4 of the 5 lectures beginning with “Simple Riemann appoximation using rectangles” at https://www.khanacademy.org/math/calculus/integral-calculus/riemann-sums/v/simple-riemann-approximation-using-rectangles (skip “Trapezoidal approximation of area under curve”)
• My mini-lecture on designing and testing programs, at https://cloud.ensemblevideo.com/app/sites/index.aspx?destinationID=IlO-D-b-vUWVkAsj2Is5Z

Exercise

Write a Matlab program that explores Riemann sums as approximations to definite integrals, as follows:

Step 1

Consider the problem of computing

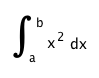
using a left Riemann sum with n equal-size intervals. What are the inputs to this problem? What is the output? Devise a couple of example instances of the problem that reflect at least one small but typical instance, and any special cases or edge cases you can think of. Solve these instances by hand.

Once you have solved your examples by hand, write a Matlab function that takes a, b, and n as parameters, and that returns an approximation to the integral using a left Riemann sum. Test your function against your examples.

Note that you can write this function without using a “for” loop.

(As a bonus question, write your function so that it integrates an arbitrary function, passed as an additional parameter, instead of always integrating x². Devise additional examples illustrating typical and special case or edge case functions, solve those examples by hand, and test your integration function on them.)

Step 2

Repeat step 1, but using a right Riemann sum instead of a left sum. In devising examples to help you understand and test this problem, be sure that at least one has a different output when done using a left sum than when done using a right sum (i.e., an example that can distinguish a left Riemann function from a right Riemann one).

The ideal way to solve this step would actually be to modify your function from step 1 so that it takes an additional parameter that determines whether it computes a left sum or a right sum. This strategy embodies a general rule of programming that I describe as “never code the same idea twice”—i.e., every time you write a piece of code you have to test it and probably debug it, so if you have to write the same basic idea in several places, you will save testing and debugging time in the long run if you write it once as a single function that can be called whenever it is needed.

Step 3

Write a Matlab script that does the following:

• Assigns values to variables a, b, and n, either by assigning constants to the variables, or by reading values from its user
• Plots, in a single graph, the function y = x² between x = a and x = b, the rectangles that would be used in a left Riemann sum approximation to the integral of x² between these bounds with n intervals, and the rectangles that would be used in a right Riemann sum approximation to the integral with n intervals.
• Prints the values of the left and right Riemann approximations.
• Prints the exact value of the integral (which is (b³ - a³) / 3).

Run this script for a range of n values, including both small values (i.e., small enough that the Riemann sums could be computed by hand) and values too large to be practical to use in hand calculations.

Step 4

Write another script that examines the error in left Riemann sums and right Riemann sums, i.e., the difference between the values they produce and the exact integral, as n increases. More specifically, your script should use left and right Riemann sums to estimate

for n values starting at perhaps n = 1 or n = 2 and ending at an n of several thousand. In a single graph, plot the left approximations, the right approximations, and the exact value, against n. Also print the relative error in the approximations (i.e., the difference between the aproximate value and the exact one, divided by the exact value; equivalently, this is the error as a fraction of the actual value).

Note that you should not use n values equally spaced between 1 or 2 and 1 or 2 thousand, since if you do you will either neglect the small values or overwhelm yourself with relative errors for the large ones, Instead, devise some way to select n values that gives you a reasonable sense of the error over the whole range without producing too much data to be intelligible.

Step 5

Matlab has two main ways of doing a computation on multiple pieces of data: writing a “for” loop, and “vectorization” (the ability of many Matlab operators, and therefore of expressions built from them, to operate simultaneously on all elements of a matrix). In your study group, discuss the relative advantages of both ways of computing on multiple values. When do you think a “for” loop is appropriate, and when do you think vectorization is?

Bonus

As a further exercise in working with “for” loops, implement the following idea for reducing the physical size of a digital image. If the original image is n rows high by m columns wide (assume both are even), an image of n/2 rows by m/2 columns can be generated by letting the brightness of the pixel in position (i,j) (meaning row i and column j) of the reduced image be the average of the brightnesses of the pixels in positions (2i-1,2j-1), (2i-1,2j), (2i,2j-1), and (2i,2j) of the original image.

Follow-Up

In your study group’s first face-to-face meeting with me following your “Complete By” date above, I will look over your solutions to the problems, ask you any further questions I have, and answer any questions from you. I may also ask you to demonstrate some of your answers in Matlab. Please bring “.m” files for each step of the lesson to your meeting. This will speed the meeting along.

If you aren’t already signed up for a study group meeting during the week following your “Complete By” date, please sign up. Make the meeting 15 minutes long, and try to make it at a time all members of your study group can attend. If no such time exists, make it at a time the greatest number of members can attend.